I.2. Variable aléatoire (VA)
Une variable est une entité qui peut prendre toutes les valeurs d’un ensemble de définition donné. On la dénommera variable aléatoire si la valeur obtenue est soumise au hasard (pile/face). Par opposition, une variable déterministe donne toujours la même valeur pour un effet donné (interrupteur arrêt/marche). Une variable aléatoire est représentée par une lettre majuscule ( X, Y, Z) alors que les valeurs prises par cette variable sont représentées par des lettres minuscules (x1, x2,... ; y1, y2,... ; z1, z2,...) (Norme AFNOR NFX 06-002)
On distingue :
-
les variables aléatoires qualitatives
-
les variable aléatoires quantitatives discontinues et continues
2.1. Variable aléatoire qualitative
C'est une variable qui porte sur des grandeurs non numériques (la couleur des cheveux, bon/défectueux). L'étude de ce type de variable s'effectue par un tableau de dénombrement en donnée brute ou en pourcentage. La complexité du tableau dépend du nombre d'entrées que l'on insère
C’est une variable qui porte sur des grandeurs non numériques (la couleur des cheveux, bon/défectueux). L’étude de ce type de variable s’effectue par un tableau de dénombrement en donnée brute ou en pourcentage. La complexité du tableau dépend du nombre d’entrées que l’on insère

2.2. Variable aléatoire quantitative discontinue ( ou VA discrète)
C’est une variable qui ne peut prendre qu’une suite discontinue (finie ou infinie) de valeurs sur l’ensemble des nombres entiers.

2.3.Variable aléatoire continue
Ce type de variable peut prendre toutes les valeurs d’un intervalle fini ou infini.
masse de produit contenue dans un flacon, âge, taille, poids, diamètre, vitesse...
Si ce type de variable est parfaitement défini d’un point de vue théorique, en pratique les valeurs prises par une variable continue dépendent de la sensibilité de l’appareil de mesure et ne peuvent être définies sur un intervalle fini ou infini de nombre réels mais arrondies avec une incertitude donnée.
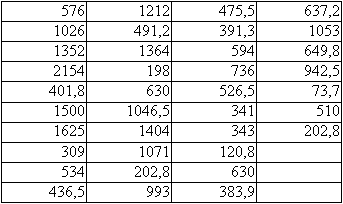
Résultats d'un dosage effectué sur les sérums de 37 sujets (résultats exprimés en milligramme par litre avec une précision absolue de 0,05 milligramme :